Let’s say you’re about to launch a new product. In this hypothetical, this means investing a million dollars on manufacturing and distribution for a first batch of product.
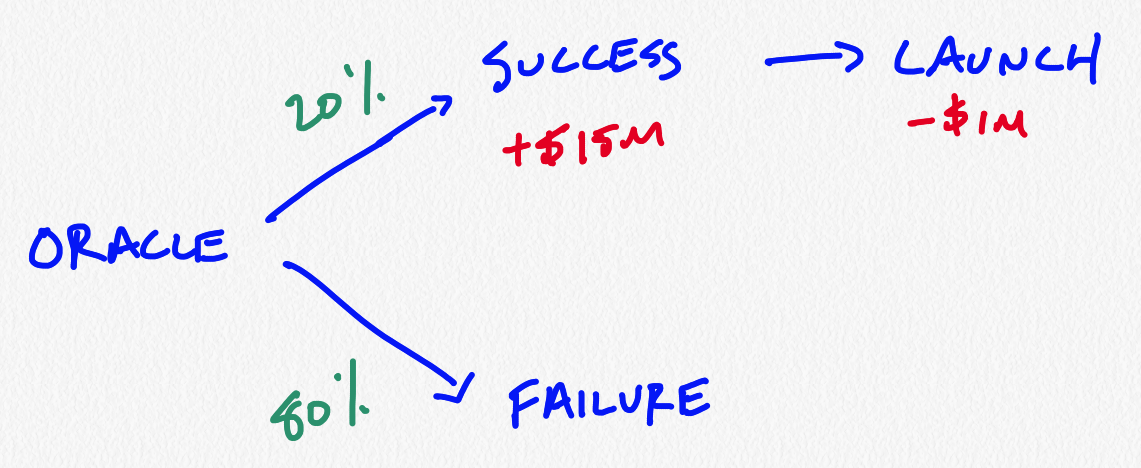
To simplify things, we’ll assume there are two possible outcomes: “success” -- you prove commercial viability of the product and sell it to a larger competitor for $15m in profit, and “failure”, where the $1m you invested is a pure loss. The probability of success is 20%. What is the value of your company?
This is easy: we can simply take the expected value:
20% * ($15 million - $1million) + 80% * ($0 million - $1 million) = $2 million
And I know this graphic is the definition of simple, but I’m going to include it here so that we can add to it below:
Now, let’s say that you had an oracle that told you the day before you cut the $1m check whether or not the product would succeed. What’s the value of your company now? Certainly higher than $2 million! But how much higher? The answer to that question is something called the “Expected Value of Perfect Information”. It’s the maximum price you’d be willing to pay for such an oracle.
I always struggle to remember how to compute this, so let me take you through my step-by-step logic. The first thing to recognize is that having an oracle doesn’t make it more likely that you’ll have a successful product, it simply means that you’ll know if it’ll be successful before you cut the check, versus after.
That means that in the equation below, the 20% and the 80% should stay in the same place as in the equation above:
20% * [$ if success guaranteed] + 80% * [$ if failure guaranteed] = $ some amount
Now all that remains is to figure out the payoffs if you knew success or failure was guaranteed. And this is easy! If you knew success was guaranteed, you’d invest the $1m right away, eagerly awaiting that $15 million payday. If you knew failure was on the horizon, you’d put the checkbook away and start working on something else.
20% * ($15 million - $1 million) + 80% * ($0) = $2.8 million
So having this oracle increases your company’s value by $800k.
But, sadly, oracles don’t exist. Only their (very) poor approximation, consultants, are what businesses have to work with. So let’s imagine that instead of traveling to Delphi, our company hires a consulting firm to give them a recommendation.
If the consulting firm gives a positive report, the product has a 50% chance of success, and if they give a negative report, the product will only have a ~3% chance of success. To fill this out, let’s say that there’s a 35% chance the consulting firm gives a positive report, and a 65% chance it gives a negative report. Can we figure out how much the consulting firm is worth?1
To figure out how much the company is worth in this hypothetical, we need to sum up all the scenarios and weight them by their probability.
p(Positive report) * [$ if positive report] + p(Negative report) * [$ if negative report]
So what is the payoff if there is a positive report? Well, there would be a 50/50 chance of success, so the payoff of launching the product is:
50% * ($15 million - $1 million) + 50% * ($0 - $1 million) = $6.5 million
What about a negative report? This is a bit more complex. First let’s look at the payoff of launching the product:
3% * ($15 million - $1 million) + 97% * ($0 - $1 million) = - $0.55 million
Okay, so if you receive a negative report, the expected payoff of launching the product is negative. So you wouldn’t launch the product and your payoff is $0.
Okay finally we can fill in the blanks above:
35% * $6.5 million + 65% * $0 = $2.275
So, in this case our consultant adds $275k of value to the company. Even though their predictions are imperfect, they are slightly better than you could do on your own.
So what is the “framework” for assessing the value of information that I promised? First we need to understand the difference between decisions and outcomes. In the decision tree above, there are decisions (“launch”, and “don’t”) and there are outcomes (“success” and “failure”). In the tree above, there are terminal outcomes (success/failure) and there are intermediate outcomes (“positive report”, “negative report”).
So to assess the value of information, you first need to draw your baseline decision tree, labeling both the decisions and outcomes. Every outcome should be associated with a probability. Any time an investment is required (e.g. with “launch”, the $1m investment) or a payoff happens (e.g. with “success”, the $15m payoff), write it down.
Once you have all this information written down, you have to move backwards from right to left and figure out, knowing what you know at that point in time, which decision you would make at each of the decision nodes. For example, if you receive a negative report, you will choose “don’t launch”. You can then prune the other branches off the tree, as they will never get travelled down.
At this point, you can then compute the probability of every path down the tree, and add up the investments and payoffs of that path, and then take the weighted average. This is your value.
With a new source of information, like the consultant, you create a new decision tree and run through the same steps. The difference in value between the new tree and the old tree is the added value of the new information.
I would expect that my readers have some questions here. For example, in my examples I said that the consultants had a 35% probability of issuing a positive report, and if they did, that the product had a 50% chance of success. In the real world, you don’t know those numbers.
Is all lost?
No, there are sophisticated ways of handling those uncertainties that involve setting prior distributions around these probabilities, and using Monte Carlo sampling to simulate the decision tree. If you’re interested in learning more, the book How to Measure Anything (specifically chapter 7) is where I got the bug.
Actually doing these formal analyses can be highly informative. With a more complicated decision tree than the ones we’ve seen, we can identify the variables that have the highest value of information, and exactly how much we would pay to reduce exactly how much of our uncertainty.
For example, you’d usher to the door any consultant proposing a fee over $800k, even without carrying the analysis we did above all the way to the end, because even perfect uncertainty reduction wouldn’t have been worth that much. And you can imagine a world where we’d play with some of the numbers I used above (e.g. that the product would have a 50% shot of success if the consultant gave a positive report) to see how much the consultant would be worth under different hypotheticals.
If you’re interested in running this sort of analysis for a major investment, please do reach out.
You can check to ensure that I didn’t cheat and make the overall chances of success: 35% * 50% + 65% * 3% = 19.5%









Cool post! Really liked your graphics!