What is the normal distribution, anyway?

It's surprisingly weird, at least in high dimensions

In my corner of the internet, folks seem to be up in arms about an article published in Scientific American “eulogizing” E.O. Wilson. I'm not going to go into any detail about the article itself, although many people that I admire found fault with it. I want to focus on one passage in which the normal distribution played a starring role. One line in particular drew the ire of many commentators, including myself:

First, the so-called normal distribution of statistics assumes that there are default humans who serve as the standard that the rest of us can be accurately measured against. 

The first thing to call out is that the normal distribution itself assumes nothing about humanity; it is simply a mathematical construct that has a bell curve shape and conveniently integrates to one.

The application of the normal distribution may be making some assumptions, but it is the people doing the application that are making these assumptions, not the distribution itself. With that out of the way, a useful question to ask is what assumptions you are making when you use the normal distribution, and does the normal distribution imply that there could be such things as a reference person that everyone else could be compared against. Let's go through each of these questions in turn.

There are many ways to derive the normal distribution, but I will focus on just one. It is useful to think of data that is described by a normal distribution as arising from a particular kind of process. That process is one in which many small things get added together. Whenever what you observe is the result of many different components adding together to result in some aggregate quantity, you will typically get a normal distribution. For example height, intelligence, running speed —  these are all examples of quantities that are influenced by innumerable genetic and environmental factors, that when added together result in an aggregate quantity, and look like a normal distribution. 

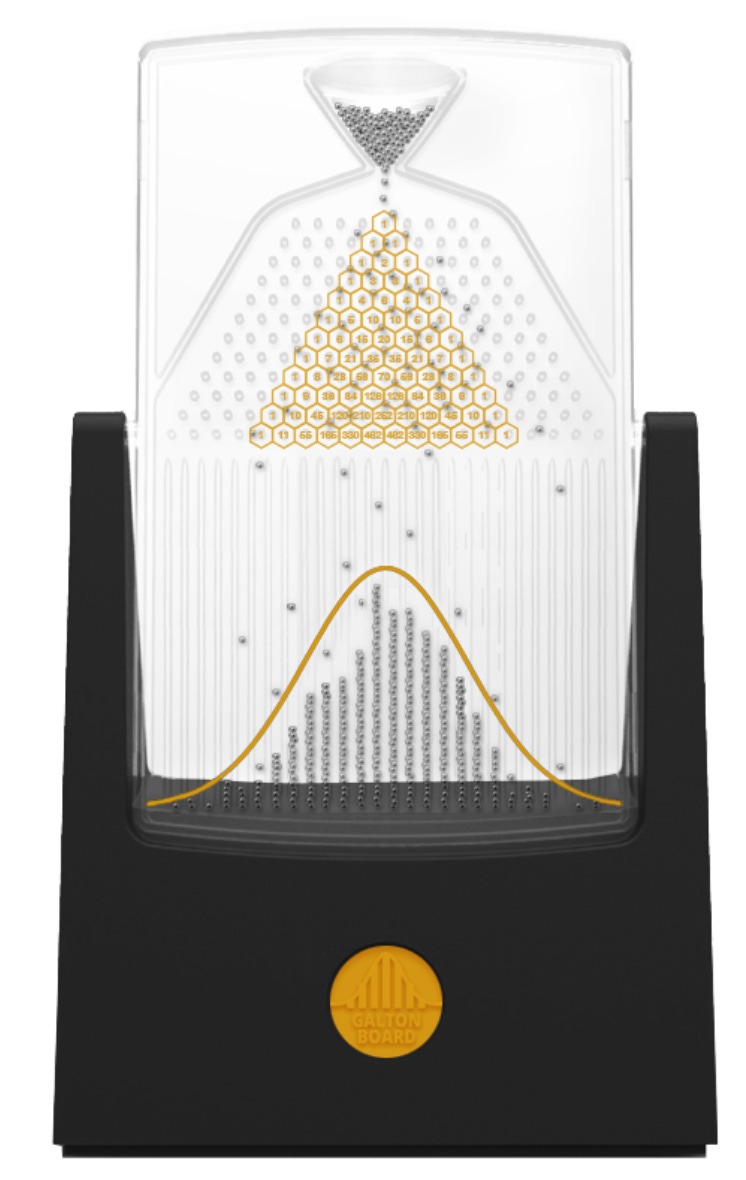
You can see the underlying process by observing the Galton board, where you drop a ball through a triangle of pins into a set of bins at the bottom. Each pin is like an on-off switch, and some balls will get pushed further to the right, and some further to the left. As you get further to the right (or left), more and more bounces will have had to have gone in the same direction, which becomes exponentially less likely. This is a physical manifestation of the fact that you can approximate the binomial distribution with a normal distribution — and vice versa. 

This derivation of the normal distribution, while not rigorous, illustrates the most important fact about the normal distribution. Namely that it has very thin tails, because to get further to the right or left in the distribution, you are combating against a process that decays exponentially. In the Galton board, to get two pins to the right, the ball needs to bounce the right way twice, the odds of which are (½)^2.  For the ball to land 4 pins to the right it needs to bounce to the right four times, which is (½)^4, and so on. You can mentally draw the rest of the line yourself. 

So far we have talked only about univariable data; that is data for which an observation can be described with a single number. Most data is multivariable. The multi-dimensional analog to the normal distribution is called the multivariable normal distribution. Whereas the single variable normal distribution only requires two numbers to give its full description, the multivariable normal distribution requires a full matrix of data, The increased data requirements arise from the need to describe the correlations between the variables in addition to their respective means and variances. 

A funny thing happens as you increase the number of dimensions. The so-called bell curve shape loses fidelity as a description of what's going on. People that work with high-dimensional data will know exactly where I'm going, and that is towards the curse of dimensionality.

As I'm about to ask you to visualize things in higher dimensions, I’m reminded of the famous quote by Goeff Hinton:

> To deal with hyper-planes in a 14-dimensional space, visualize a 3-D space and say 'fourteen' to yourself very loudly. Everyone does it.

In one dimension, the normal distribution is a simple bell curve. In two dimensions it can be described as something like a hill being viewed from above. And in three dimensions, we start to run out of space. Instead of plotting the density of the distribution (which requires adding a dimension to the underlying data, which is why a bell curve needs two dimensions to be plotted), we have to resort to a 3D scatterplot. 

Keeping this image in your mind, let’s increase the number of dimensions. You can't visualize it directly, so don't try — just stick with three. Let's imagine our data as an orange, with a fleshy interior and a skin. In three dimensions most of the data in your scatter plot will be in the fleshy interior. Some even close to the very center. But as you increase the number of dimensions, your data is going to move out of the interior and into the skin. 

Why is this happening? In a way, the reasoning is very similar to why, in a single variable normal distribution, it gets harder to move into the tails. Most people that have taken statistics know that the area under the curve within one standard deviation of the mean is about 68%. So to be close to the center in a single variable distribution, your weighted coin flip, weighted such that it comes up heads 68% of the time, only needs to come up heads once. In a two-dimensional normal distribution, this coin needs to come up heads twice, and in a 100 dimensional normal distribution, it needs to come up heads 100 times. That is, the odds that you will be within one standard deviation of the mean on every variable will be 0.68^100, or a number that has seventeen zeros after the decimal point. So as you increase the number of dimensions under analysis, the likelihood that any data point will be close to its average becomes vanishingly small.

So while it is true that the application of the normal distribution to any single variable describing humans will necessarily assume then on any single dimension there is a central tendency, or some reference point that could usefully described as the average person, it is not the case that the same application of the normal distribution to multi-dimensional data will make the same assumption. In fact, to assume that there is something usefully thought of as a reference point in high dimensions, you have to make very strong additional assumptions.